Vega (v): what does this Greek stand for with options

There are several factors which impact on the option’s prices and one of them is implied volatility. Let’s take a look at the Vega which is directly connected to it and discover the purpose of this Greek in the market.

Options & v

Vega (ν) is the Greek which stands for measuring the influence of expected volatility on the option. Basically, it is a 1% or a one-point change of the cost. The volatility’s value is usually an integer number.Importantly, v is not exactly the extent of the price movements which happened in the past or in the future. It is that special one which measures the influence of a future volatility on the cost. Let’s take a look at the example of chart:

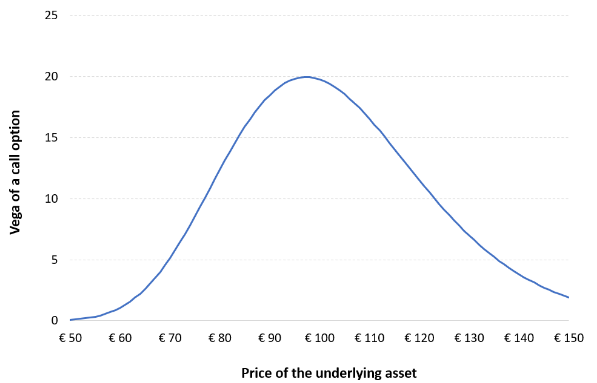
Vega-neutral strategies

Decrease or eradication of the expected volatility’s impact: that’s what Vega-neutral strategies stand for. By using them, you can insulate options off the possible sharp changes in the extents of the cost’s movements and allow you to pay more attention to other factors which also impact on the cost. Let’s take a look at the example.Vega-neutral spread. It is all about the balance between positive and negative v values which is supported by long and short options together. For instance, a market player buys several at-the-money assets and sells some out-of-the-money ones with the same validity period. The choice must be very accurate: number of contract and strike prices must fit in to equal both of v values or at least to make the net v value around 0. In more detail, two at-the-money options with v=0.10 and four out-of-the-money with v=-0.05: in this case, the market player equalises these v values.

The following equation will look like this: (2 × 0.10) - (4 × 0.05) = 0

That's one way to get the vega-neutral position. It provides a relatively stable condition of the price in case the expected extent of the cost movements changes.These strategies are for advanced traders because they are very demanding in constant observations, optimal risk management, and several adjustments during the whole trading period. In addition, let’s take look at the instance of the calendar spreads:

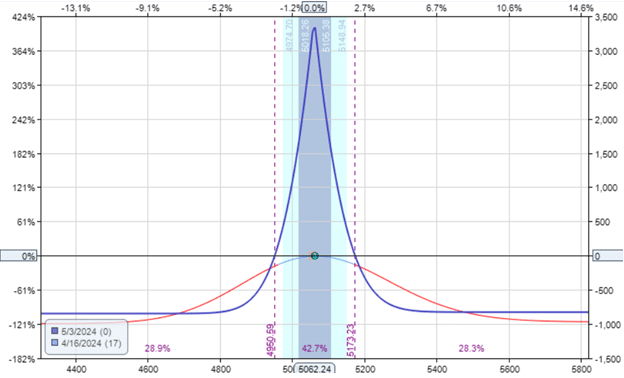
The relationship between Vega and volatility

First of all, volatility stands for the amount and velocity of the cost movements and can be based on the latest valuation fluctuations, changes in the past and potential valuation movements in the future. Assets which expire in the future have a positive v and the ones which expire very soon have a negative v. It is explained by the premium amount which is assigned by traders. The more they offer - the higher the v and they assign more for those which expire in a longer-term perspective.If there’s more uncertainty about the future cost movement it makes the asset more valuable. Options which are at-the-money and with a longer-term validity period are these desirable choices. The closer it gets to the expiration date, the lower the v because of a constant reduction of the volatility influence in the future.

Instance of v

Let’s review the instance.More detailed, the valuation is $1.50 with vol at %15. With v=0.10, increase or decrease of volatility by 1%, the price will be $1.60 or $1.40, respectively.

The reason behind the “Vega” naming

There is no exact explanation of the “Vega” naming. It isn’t directly related to the Greek alphabet. The most common story behind this includes several early option traders or financial scientists. In this scenario, they invented and applied “vega” as a pseudo-Greek term. Throughout the time, it took root within the market. Now “vega” is a widely-used term which stands for an influence of the extent of the price movements on the cost itself. v is rightfully stated with in the table of Greeks below:

Identifying market’s sentiment with Vega

Vega can help to determine market sentiment. If v is high, it means a huge amount of changes and instability in the market. It usually occurs at the time of global economic announcements or in the period of earnings. On the other hand, if v is low, expected changes won’t be so significant and the market is considered stable within such time periods.

Theta (Θ) & Vega (v)

Let’s take a look at both of v and Θ:

• v is the change in cost which is connected to a 1% change in expected volatility. It is being calculated with the following formula:

• Θ is the valuation’s decrease velocity in relation to the time. Also known as time decay. The calculator formula:

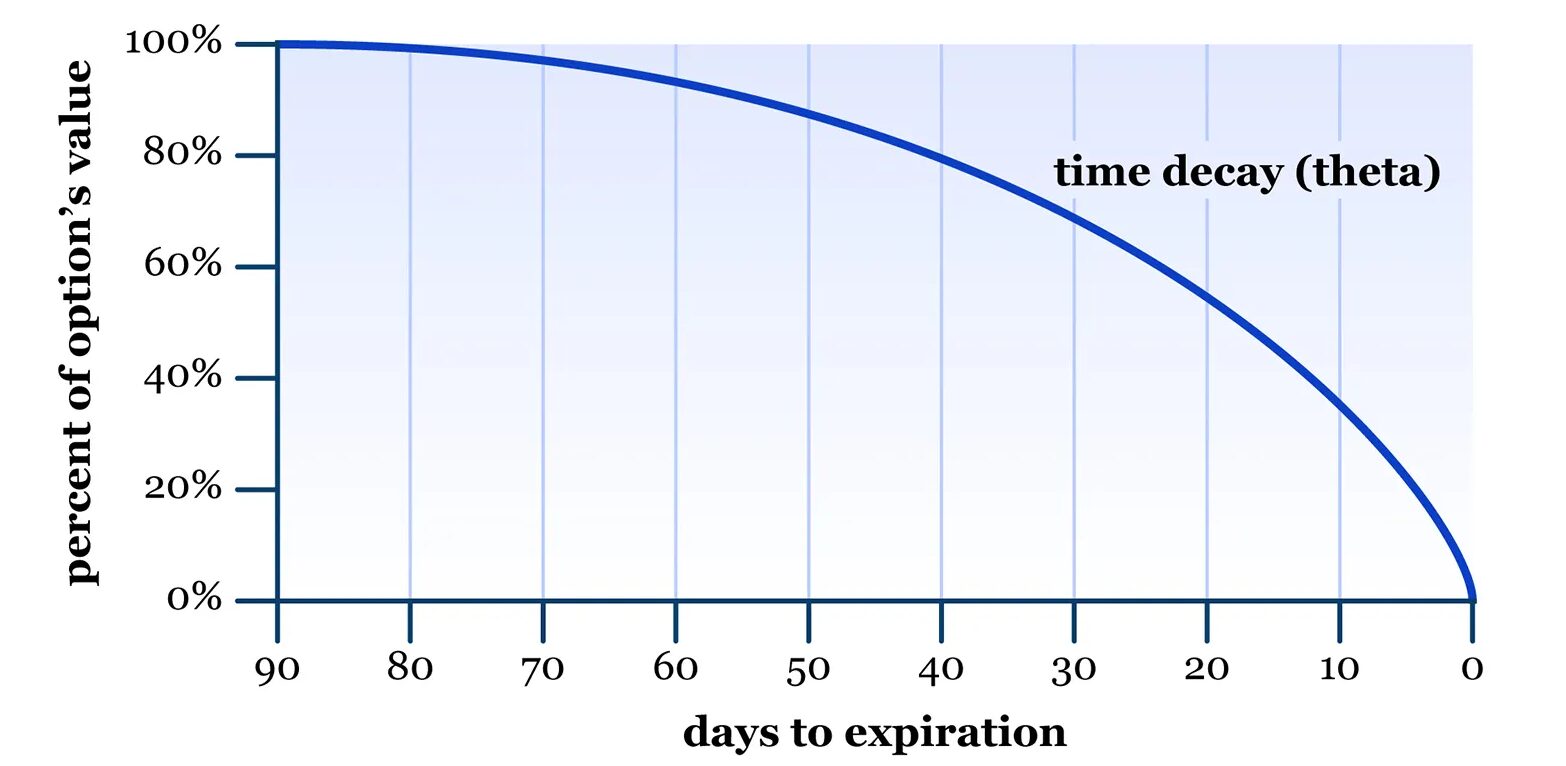
In addition, here’s what the theta chart looks like:Relationship between these two is quite obvious. More time to move - more opportunities to change. The unpredictability and possibilities play the main role. The more time an asset has - the higher the v will be. In opposition, the less time left - the lower is the v. It is explained simply: the possible impact reduces because of the expiration date. There will be nothing to influence on in the end, so that’s the principle.

The impact of the expected volatility on the options valuations

Cost increases under the impact of the expected volatility. It is based on the principle of probability of the option’s price to end in the money. The price will increase together with the extent of its movements. That’s why it is commonly followed by finishing in the money on the expiration date.